hp 41CX (その２)

2012年11月8日コブタイカ関数電卓コメントを受け付けていません

検索サイトで「HP 41シリーズ」を検索すると、結構検索結果に引っかかるのが、「ロケットガール」である。

ロケットガール表紙

この「ロケットガール」は、1995年に発行されたライトノベル作品です。
発行は富士見書房（富士見ファンタジア文庫）。
原作は野尻抱介氏。
作品の内容は、女子高生がひょんなことから宇宙飛行士となり、その訓練風景から活躍を描いたSF作品です。

「ロケットガール」は、2007年にWOWOWでアニメ版が放送され、ライトノベルを読んでいない方でもアニメは観たという方もいらっしゃるのではないでしょうか。

さて、HP 41CXのその２でこの作品を紹介したのは、この作品の中でHPの電卓が登場している場面があるからなんですね。

HP電卓ファンの方はもうとっくにご存知だと思いますが、アニメ版だと第二話「アッセンブリ -assembly-」にHP 41Cが登場します。

その時の劇中の会話は以下の通りです。

ロケットガール１

木下和也（教官）　「では、宇宙航行学の授業を始める。軌道制御の基本は、ホーマントランスファー。そしてこれがその方程式だ。この初期値と定数で計算してみろ。」
森田ゆかり（主人公、女子高生）　「は？」
教官　「どうした。デルタV1とデルタV2の値は？」
ゆかり　「でもその数字、７桁もあるし・・・。」
教官　「電卓があるだろ！」
ゆかり　「うぁ～あ！そうか、そうか。ぅぁ、何これ。イコールがないじゃん！」
教官　「あったりまえだ！逆ポーランド演算を知らんのか！」

ゆかり　「知るわけないじゃん！」

ロケットガール２

ドン！（教壇を叩く音）

ゆかり　「ひぇ！」
教官　「おぉー、そうか！ならば今から５分で操作を叩き込む。二度と普通の電卓は使えない体にしてやるから、覚悟しろ！」
ゆかり　「はぁ～？？？」

これは「その筋の方々」には非常に有名な場面ですｗｗｗ。

まあ、今の工学部の学生ですらRPN（逆ポーランド演算）を知らない人達が多々居ると思うので、女子高生の主人公が知らなくても当たり前ですよねｗ。

ということで、せっかくなので今回はこの「ホーマントランスファー（軌道）」を劇中通りHP 41CXで解いてみましょう。

まず、このホーマントランスファー（軌道）ですが、これについて調べてみました。

いつもお世話になっているWikipedia大先生によると、「ホーマン遷移軌道（Hohmann transfer orbit）」は、ドイツのヴァルター・ホーマンが1925年に発表した「同一軌道面にある2つの円軌道の間で軌道を変更するための遷移軌道」のことです。

ホーマントランスファー軌道

そして、ホーマン遷移軌道は、「2つの円軌道の間を最も少ないエネルギーで移動することができる。また、近日点と遠日点の2回だけしか速度変化を必要としない。」という、宇宙空間での軌道変更の計算の考え方であるという事ですね。

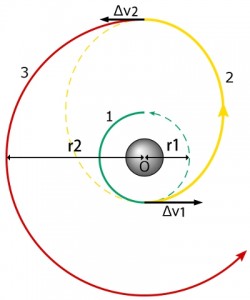
右図によると、緑色で示された１の軌道から赤で示された３の軌道へ遷移するときの、黄色で示された２の軌道を行うための計算という事になります。

なるほど。半径 $r1$ の１の軌道のある時点で速度を $\Delta v1$ にしてやると、１の軌道から外れて２のような軌道になる。
そして、希望する半径 $r2$ の３の軌道上に来たとき、速度を $\Delta v2$ にしてやると上手い具合に３の軌道に乗るというものなのかなｗ。

それで、上の図で示したように、教官がホワイトボードに記述した定数と式を以下に記すと、

$\displaystyle{\mu E = 3.986005E5 \hspace{30pt} (=3.986005 \times 10^{5} [km^{3}/s^{2}])}$
$r1 = 6778 km$
$r2 = 9378 km$

$\displaystyle{a = \frac{(r1+r2)}{2}}$

$\displaystyle{V_{1} = \sqrt{\frac{\mu E}{r1}}}\hspace{30pt} \displaystyle{V_{p1} = \sqrt{\frac{\mu E}{r1}} \sqrt{\frac{2 \times r2}{r1+r2}}}$

$\Delta V1= V_{p1} - V_{1}$

$\displaystyle{V_{2} = \sqrt{\frac{\mu E}{r2}}}\hspace{30pt} \displaystyle{V_{p2} = \sqrt{\frac{\mu E}{r2}} \sqrt{\frac{2 \times r1}{r1+r2}}}$

$\Delta V2 = V_{2} - V_{p2}$

になります。ホワイトボードでは、 $\displaystyle{\nabla 1 (or 2)}$ となっていますが、 $V$ の間違いでしょうねｗ。また、上式では、足りないだろうなぁ・・・っていう添え字などを付け加えています。

そして教官は、上式を用いて $\Delta V1$ と $\Delta V2$ を求めなさい、と言っているのですね。

ここで、 $\mu E$ は、「標準重力パラメータ（Standard gravitational parameter）」と呼ばれる定数（ $km^{3} s^{-2}$ ）です。
$a$ は平均半径（使っていませんが・・・）、 $r1$ および $r2$ は軌道遷移前後の半径を表します（それぞれ $km$ ）。

これを、ゆかりさんはHP 41Cで計算しなければなりません。
ま、使い慣れている人なら全く難しい計算ではないですｗｗｗ。

では、実際にやってみましょう！
上記式程度の計算では、電卓を使う上で特殊なテクニックは必要ないと思います。現在普通に販売されている電卓でも $\sqrt{\hspace{5pt} }$ の計算くらいは当たり前のように付いていますので、HP 41CXで計算を行う必要はないですよねｗ。

しかし、開発日和・・・では、敢えてHP 41CXで計算することにします！

RPNが利用できるHP電卓の楽しさは、計算をするときに「その順序」をまず考えるところにあります。
現在市販されている電卓は、数式の順序通りに入力して、最後に＝キーを押すと簡単に計算結果を得ることが出来ます。
しかし、この方法だとキーストロークが若干多くなるのです。また、見た目通りに入力するため、「式の評価」というものを全く考えなくなります。

その点RPN方式の電卓では、どの順番で計算するのがもっとも効率的で正しく行えるのか・・・、を考えなければなりません。ここがHP関数電卓の面白いところですね。

前置きが長くなりましたが、実際に計算してみましょう。

$V1$ については、特に考える必要は無いですね。そのまま、普通に計算します。

１）　3.986005 > [EEX] > 5 > [ENTER]　・・・　Yスタックに記憶させる
２）　6778 > [÷]　・・・　これで $3.986005E5 \div 6778$ の結果58.8080がXレジスタに入る
３）　 $[\sqrt{x} ]$ 　・・・　これで $\sqrt{58.8080}$ の結果がXレジスタに入る
４）　 $V_{1} = 7.6686 \hspace{5pt} (km/sec)$

実機をお持ちの方は、この状態で $[ R \downarrow ]$ キーを何度か押してみてください。
HP 41CXは、スタックが４段あります。今液晶に表示されているスタックはXレジスタです。３）の計算が終わった直後では、表示されているXレジスタ以外のレジスタには「0.0000」のように0の値がスタックされていると思います。

ここで、次に $V_{p1}$ を計算するのですが、この式中には $V_{1}$ の結果が含まれて居ます。
ですので、[ENTER]キーをもう一度押して、Yレジスタにも求めた $V_{1}$ の結果をスタックさせておきます。

５）　[ENTER]　・・・　 $V_{1}$ の値をYレジスタにもスタックさせておく

次に $V_{p1}$ の計算を行います。これも普通どおり計算したほうがよさそうですね。

６）　2 > [ENTER] > 9378 (r2) > $[\times ]$ 　・・・　 $\sqrt{\hspace{5pt}}$ の中の分子の計算
７）　6778 (r1) > [ENTER] > 9378 (r2) > [+]　・・・　 $\sqrt{\hspace{5pt}}$ の中の分母の計算
８）　 $[\div ]$ 　・・・　 $\sqrt{\hspace{5pt}}$ の中の割り算まで計算
９）　 $[\sqrt{x} ]$ > $[\times ]$ 　・・・　ここまでで $V_{p1}$ の計算
10）　 $V_{p1} = 8.2627 \hspace{5pt} (km/sec)$
11）　 $[x\bowtie y] > [-]$ 　・・・　この操作は、Yレジスタに $V_{1}$ 、Xレジスタに $V_{p1}$ の値が入っているため、まずXレジスタとYレジスタの値を交換して引き算しました。（注： $[x\bowtie y]$ キーは、 $\LaTeX$ にHP 41CXで使われているキー表示がなかったため、このようにしました。このキーは、 $[\Sigma + ]$ キーの直ぐ下にあるXYレジスタ入れ替えキーです。）
12）　0.5941 $(km/sec)$ 　・・・　最後に液晶画面に表示された値。これが $\Delta V1$ です。